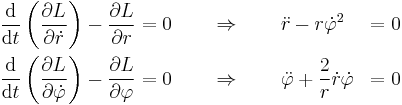Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a functional which takes the trajectory (also called path or history) of the system as its argument and returns a real number as the result. Action has units of energy × time (joule-seconds in SI units), the same as Planck's constant or angular momentum. Generally, the action takes different values for different paths. Classical mechanics postulates that the path actually followed by a real physical system is that for which the action is minimized (or, more strictly, is stationary). The classical (differential) equations of motion of a system can be derived from this principle of least action. The stationary action formulation of classical mechanics extends readily to quantum mechanics in the Feynman path integral formulation, where a physical system follows simultaneously all possible paths with amplitudes determined by the action. It also provides a basis for the development of string theory.
If the action is represented as an integral over time, taken along the path of the system between the initial time and the final time of the development of the system,
the integrand,  , is called the Lagrangian. For the action integral to be well defined the trajectory has to be bounded in time and space.
, is called the Lagrangian. For the action integral to be well defined the trajectory has to be bounded in time and space.
History of term action
The term action was defined in several (now obsolete) ways during its development.
- Gottfried Leibniz, Johann Bernoulli and Pierre Louis Maupertuis defined the action for light as the integral of its speed (or inverse speed) along its path length.
- Leonhard Euler (and, possibly, Leibniz) defined action for a material particle as the integral of the particle's speed along its path through space.
- Pierre Louis Maupertuis introduced several ad hoc and contradictory definitions of action within a single article, defining action as potential energy, as virtual kinetic energy, and as a hybrid that ensured conservation of momentum in collisions.[1]
Concepts
Physical laws are most often expressed as differential equations, which specify how a physical quantity varies over infinitesimally small changes in time, position, or other independent variable in its domain. A differential equation provides the value of the physical variable at any point in its domain, given some initial conditions.
In analytical dynamics, the action represents the final form obtained by working backwards from classical Newtonian mechanics to achieve an integral minimization expression in the form of a variational statement. The statement is profound, simple, and elegant but comes at the cost of several simplifying assumptions. The integral form espoused here can only be applied to conservative holonomic mechanical systems and to do otherwise can yield incorrect results.
The equivalence of these two approaches is contained in Hamilton's principle, which states that the differential equations of motion for any physical system can be re-formulated as an equivalent integral equation. It applies not only to the classical mechanics of a single particle, but also to classical fields such as the electromagnetic and gravitational fields.
Hamilton's principle has also been extended to quantum mechanics and quantum field theory.
Mathematical definition
Expressed in mathematical language, using the calculus of variations, the evolution of a physical system (i.e., how the system actually progresses from one state to another) corresponds to a stationary point (usually, a minimum) of the action.
Several different definitions of 'the action' are in common use in physics:
- The action is usually an integral over time. But for action pertaining to fields, it may be integrated over spatial variables as well. In some cases, the action is integrated along the path followed by the physical system.
- The evolution of a physical system between two states is determined by requiring the action be minimized or, more generally, be stationary for small perturbations about the true evolution. This requirement leads to differential equations that describe the true evolution.
- Conversely, an action principle is a method for reformulating differential equations of motion for a physical system as an equivalent integral equation. Although several variants have been defined (see below), the most commonly used action principle is Hamilton's principle.
- An earlier, less informative action principle is Maupertuis' principle, which is sometimes called by its (less correct) historical name, the principle of least action.
Disambiguation of "action" in classical physics
In classical physics, the term "action" has at least eight distinct meanings.
Action (functional)
Most commonly, the term is used for a functional  which takes a function of time and (for fields) space as input and returns a scalar. In classical mechanics, the input function is the evolution
which takes a function of time and (for fields) space as input and returns a scalar. In classical mechanics, the input function is the evolution  of the system between two times
of the system between two times  and
and  , where
, where 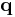 represent the generalized coordinates. The action
represent the generalized coordinates. The action ![\mathcal{S}[\mathbf{q}(t)]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/b3c291e94128405fd44791176583e4d1.png) is defined as the integral of the Lagrangian
is defined as the integral of the Lagrangian 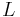 for an input evolution between the two times
for an input evolution between the two times
where the endpoints of the evolution are fixed and defined as  and
and 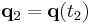 . According to Hamilton's principle, the true evolution
. According to Hamilton's principle, the true evolution 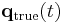 is an evolution for which the action
is an evolution for which the action ![\mathcal{S}[\mathbf{q}(t)]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/b3c291e94128405fd44791176583e4d1.png) is stationary (a minimum, maximum, or a saddle point). This principle results in the equations of motion in Lagrangian mechanics.
is stationary (a minimum, maximum, or a saddle point). This principle results in the equations of motion in Lagrangian mechanics.
Abbreviated action (functional)
Usually denoted as 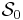 , this is also a functional. Here the input function is the path followed by the physical system without regard to its parameterization by time. For example, the path of a planetary orbit is an ellipse, and the path of a particle in a uniform gravitational field is a parabola; in both cases, the path does not depend on how fast the particle traverses the path. The abbreviated action
, this is also a functional. Here the input function is the path followed by the physical system without regard to its parameterization by time. For example, the path of a planetary orbit is an ellipse, and the path of a particle in a uniform gravitational field is a parabola; in both cases, the path does not depend on how fast the particle traverses the path. The abbreviated action 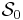 is defined as the integral of the generalized momenta along a path in the generalized coordinates
is defined as the integral of the generalized momenta along a path in the generalized coordinates
According to Maupertuis' principle, the true path is a path for which the abbreviated action 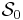 is stationary.
is stationary.
Hamilton's principal function
Hamilton's principal function is defined by the Hamilton–Jacobi equations (HJE), another alternative formulation of classical mechanics. This function  is related to the functional
is related to the functional  by fixing the initial time
by fixing the initial time  and endpoint
and endpoint 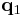 and allowing the upper limits
and allowing the upper limits  and the second endpoint
and the second endpoint  to vary; these variables are the arguments of the function
to vary; these variables are the arguments of the function  . In other words, the action function
. In other words, the action function  is the indefinite integral of the Lagrangian with respect to time.
is the indefinite integral of the Lagrangian with respect to time.
Hamilton's characteristic function
When the total energy  is conserved, the HJE can be solved with the additive separation of variables
is conserved, the HJE can be solved with the additive separation of variables
 ,
,
where the time independent function 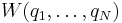 is called Hamilton's characteristic function. The physical significance of this function is understood by taking its total time derivative
is called Hamilton's characteristic function. The physical significance of this function is understood by taking its total time derivative
 .
.
This can be integrated to give
 ,
,
which is just the abbreviated action.
Other solutions of Hamilton–Jacobi equations
The Hamilton–Jacobi equations are often solved by additive separability; in some cases, the individual terms of the solution, e.g.,  , are also called an "action".
, are also called an "action".
Action of a generalized coordinate
This is a single variable 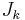 in the action-angle coordinates, defined by integrating a single generalized momentum around a closed path in phase space, corresponding to rotating or oscillating motion
in the action-angle coordinates, defined by integrating a single generalized momentum around a closed path in phase space, corresponding to rotating or oscillating motion
The variable 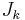 is called the "action" of the generalized coordinate
is called the "action" of the generalized coordinate  ; the corresponding canonical variable conjugate to
; the corresponding canonical variable conjugate to 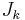 is its "angle"
is its "angle"  , for reasons described more fully under action-angle coordinates. The integration is only over a single variable
, for reasons described more fully under action-angle coordinates. The integration is only over a single variable  and, therefore, unlike the integrated dot product in the abbreviated action integral above. The
and, therefore, unlike the integrated dot product in the abbreviated action integral above. The 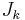 variable equals the change in
variable equals the change in  as
as  is varied around the closed path. For several physical systems of interest,
is varied around the closed path. For several physical systems of interest, 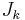 is either a constant or varies very slowly; hence, the variable
is either a constant or varies very slowly; hence, the variable 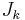 is often used in perturbation calculations and in determining adiabatic invariants.
is often used in perturbation calculations and in determining adiabatic invariants.
Action for a Hamiltonian flow
See tautological one-form.
Euler–Lagrange equations for the action integral
As noted above, the requirement that the action integral be stationary under small perturbations of the evolution is equivalent to a set of differential equations (called the Euler–Lagrange equations) that may be determined using the calculus of variations. We illustrate this derivation here using only one coordinate, x; the extension to multiple coordinates is straightforward.
Adopting Hamilton's principle, we assume that the Lagrangian L (the integrand of the action integral) depends only on the coordinate x(t) and its time derivative dx(t)/dt, and may also depend explicitly on time. In that case, the action integral can be written
where the initial and final times ( and
and  ) and the final and initial positions are specified in advance as
) and the final and initial positions are specified in advance as 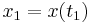 and
and 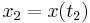 . Let
. Let 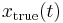 represent the true evolution that we seek, and let
represent the true evolution that we seek, and let  be a slightly perturbed version of it, albeit with the same endpoints,
be a slightly perturbed version of it, albeit with the same endpoints, 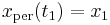 and
and  . The difference between these two evolutions, which we will call
. The difference between these two evolutions, which we will call 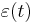 , is infinitesimally small at all times
, is infinitesimally small at all times
At the endpoints, the difference vanishes, i.e.,  .
.
Expanded to first order, the difference between the actions integrals for the two evolutions is
Integration by parts of the last term, together with the boundary conditions  , yields the equation
, yields the equation
The requirement that  be stationary implies that the first-order change
be stationary implies that the first-order change  must be zero for any possible perturbation
must be zero for any possible perturbation 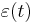 about the true evolution. This can be true only if
about the true evolution. This can be true only if
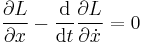 Euler–Lagrange equation
Euler–Lagrange equation
Those familiar with functional analysis will note that the Euler–Lagrange equations simplify to
 .
.
The quantity  is called the conjugate momentum for the coordinate x. An important consequence of the Euler–Lagrange equations is that if L does not explicitly contain coordinate x, i.e.
is called the conjugate momentum for the coordinate x. An important consequence of the Euler–Lagrange equations is that if L does not explicitly contain coordinate x, i.e.
- if
 , then
, then  is constant.
is constant.
In such cases, the coordinate x is called a cyclic coordinate, and its conjugate momentum is conserved.
Example: Free particle in polar coordinates
Simple examples help to appreciate the use of the action principle via the Euler–Lagrangian equations. A free particle (mass m and velocity v) in Euclidean space moves in a straight line. Using the Euler–Lagrange equations, this can be shown in polar coordinates as follows. In the absence of a potential, the Lagrangian is simply equal to the kinetic energy
in orthonormal (x,y) coordinates, where the dot represents differentiation with respect to the curve parameter (usually the time, t). In polar coordinates (r, φ) the kinetic energy and hence the Lagrangian becomes
The radial r and φ components of the Euler–Lagrangian equations become, respectively
The solution of these two equations is given by
for a set of constants a, b, c, d determined by initial conditions. Thus, indeed, the solution is a straight line given in polar coordinates.
Action principle for single relativistic particle
When relativistic effects are significant, the action of a point particle of mass m traveling a world line C parameterized by the proper time 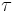 is
is
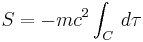 .
.
If instead, the particle is parameterized by the coordinate time t of the particle and the coordinate time ranges from t1 to t2, then the action becomes
where the Lagrangian is
 .[2]
.[2]
Action principle for classical fields
The action principle can be extended to obtain the equations of motion for fields, such as the electromagnetic field or gravity.
The Einstein equation utilizes the Einstein-Hilbert action as constrained by a variational principle.
The path of a body in a gravitational field (i.e. free fall in space time, a so called geodesic) can be found using the action principle.
Action principle in quantum mechanics and quantum field theory
In quantum mechanics, the system does not follow a single path whose action is stationary, but the behavior of the system depends on all permitted paths and the value of their action. The action corresponding to the various paths is used to calculate the path integral, that gives the probability amplitudes of the various outcomes.
Although equivalent in classical mechanics with Newton's laws, the action principle is better suited for generalizations and plays an important role in modern physics. Indeed, this principle is one of the great generalizations in physical science. In particular, it is fully appreciated and best understood within quantum mechanics. Richard Feynman's path integral formulation of quantum mechanics is based on a stationary-action principle, using path integrals. Maxwell's equations can be derived as conditions of stationary action.
Action principle and conservation laws
Symmetries in a physical situation can better be treated with the action principle, together with the Euler–Lagrange equations, which are derived from the action principle. An example is Noether's theorem, which states that to every continuous symmetry in a physical situation there corresponds a conservation law (and conversely). This deep connection requires that the action principle be assumed.
Modern extensions of the action principle
The action principle can be generalized still further. For example, the action need not be an integral because nonlocal actions are possible. The configuration space need not even be a functional space given certain features such as noncommutative geometry. However, a physical basis for these mathematical extensions remains to be established experimentally.
See also
- Lagrangian
- Lagrangian mechanics
- Noether's theorem
- Hamiltonian mechanics
- Calculus of variations
- Functional derivative
- Functional integral
- Path integral formulation
- Quantum physics
- Planck's constant
- Entropy (the least Action Principle and the Principle of Maximum Probability or Entropy could be seen analogous)
Notes
- ↑ Œuvres de Mr de Maupertuis (pre-1801 Imprint Collection at the Library of Congress.
- ↑ L.D. Landau and E.M. Lifshitz The Classical Theory of Fields Addison-Wesley 1971 sec 8.p.24-25
References
For an annotated bibliography, see Edwin F. Taylor [1] who lists, among other things, the following books
- Cornelius Lanczos, The Variational Principles of Mechanics (Dover Publications, New York, 1986). ISBN 0-486-65067-7. The reference most quoted by all those who explore this field.
- L. D. Landau and E. M. Lifshitz, Mechanics, Course of Theoretical Physics (Butterworth-Heinenann, 1976), 3rd ed., Vol. 1. ISBN 0-7506-2896-0. Begins with the principle of least action.
- Thomas A. Moore "Least-Action Principle" in Macmillan Encyclopedia of Physics (Simon & Schuster Macmillan, 1996), Volume 2, ISBN 0-02-897359-3, OCLC 35269891, pages 840 – 842.
- David Morin introduces Lagrange's equations in Chapter 5 of his honors introductory physics text. Concludes with a wonderful set of 27 problems with solutions. A draft of is available at [2]
- Gerald Jay Sussman and Jack Wisdom, Structure and Interpretation of Classical Mechanics (MIT Press, 2001). Begins with the principle of least action, uses modern mathematical notation, and checks the clarity and consistency of procedures by programming them in computer language.
- Dare A. Wells, Lagrangian Dynamics, Schaum's Outline Series (McGraw-Hill, 1967) ISBN 0-07-069258-0, A 350 page comprehensive "outline" of the subject.
- Robert Weinstock, Calculus of Variations, with Applications to Physics and Engineering (Dover Publications, 1974). ISBN 0-486-63069-2. An oldie but goodie, with the formalism carefully defined before use in physics and engineering.
- Wolfgang Yourgrau and Stanley Mandelstam, Variational Principles in Dynamics and Quantum Theory (Dover Publications, 1979). A nice treatment that does not avoid the philosophical implications of the theory and lauds the Feynman treatment of quantum mechanics that reduces to the principle of least action in the limit of large mass.
- Edwin F. Taylor's page [3]
- Principle of least action interactive Excellent interactive explanation/webpage

![\mathcal{S}[\mathbf{q}(t)] = \int_{t_1}^{t_2} L[\mathbf{q}(t),\dot{\mathbf{q}}(t),t]\, \mathrm{d}t](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/ed1d2492f39299a56130de7a20819be1.png)
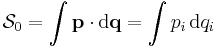


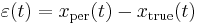
![\begin{align}
\delta \mathcal{S} &= \int_{t_1}^{t_2}\;
\left[ L(x_{\mathrm{true}}+\varepsilon,\dot x_{\mathrm{true}} +\dot\varepsilon,t)- L(x_{\mathrm{true}},\dot x_{\mathrm{true}},t) \right]dt \\
&= \int_{t_1}^{t_2}\;
\left(\varepsilon{\partial L\over\partial x} +
\dot\varepsilon{\partial L\over\partial \dot x} \right)\,\mathrm{d}t
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/b2f5d96b6a5e170d7012b7ae0ebe82e6.png)